hasfire.blogg.se - Left tailed hypothesis test calculator

#LEFT TAILED HYPOTHESIS TEST CALCULATOR SOFTWARE#

#LEFT TAILED HYPOTHESIS TEST CALCULATOR SOFTWARE#

It can be shown using statistical software that the P-value is 0.0127.

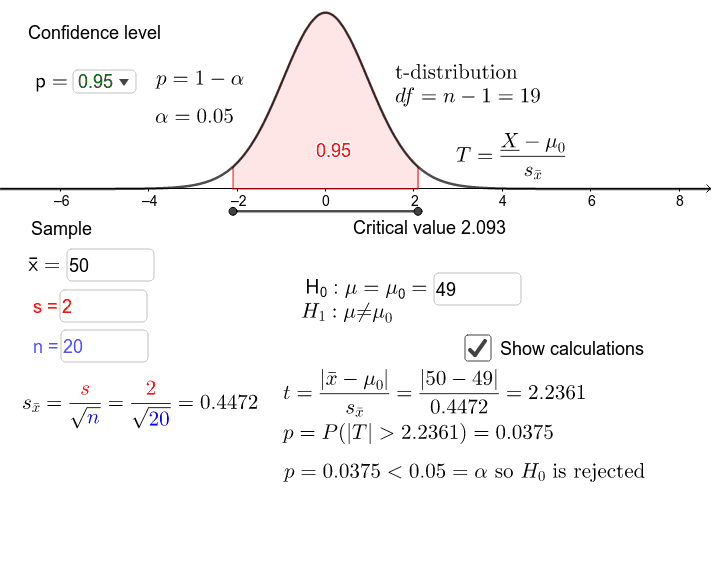
The P-value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. The P-value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t* = -2.5 if the population mean μ really were 3. In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead equaling -2.5. Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P-value, 0.0127, is then greater than \(\alpha\) = 0.01. That is, since the P-value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3. Therefore, our initial assumption that the null hypothesis is true must be incorrect. The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of H A if the null hypothesis were true. The P-value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t* = 2.5. Recall that probability equals the area under the probability curve. The P-value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t* = 2.5 if the population mean \(\mu\) really were 3. Also, suppose we set our significance level α at 0.05, so that we have only a 5% chance of making a Type I error. Since n = 15, our test statistic t* has n - 1 = 14 degrees of freedom. In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t* equaling 2.5. If the P-value is greater than \(\alpha\), do not reject the null hypothesis. If the P-value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis.

Set the significance level, \(\alpha\), the probability of making a Type I error to be small - 0.01, 0.05, or 0.10.

Using the known distribution of the test statistic, calculate the P -value: "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?").

Again, to conduct the hypothesis test for the population mean μ, we use the t-statistic \(t^*=\frac\) which follows a t-distribution with n - 1 degrees of freedom.

Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic.

Specify the null and alternative hypotheses.

Specifically, the four steps involved in using the P-value approach to conducting any hypothesis test are: And, if the P-value is greater than \(\alpha\), then the null hypothesis is not rejected. If the P-value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. If the P-value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P-value is large, say more than \(\alpha\), then it is "likely." The P-value approach involves determining "likely" or "unlikely" by determining the probability - assuming the null hypothesis were true - of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed.